一次関数は式を求める問題・図形問題・文章問題と色々なパターンの問題がありますが、その中でも正方形を使った一次関数の問題は難易度高めです。
解放の手順としては、
- まずは2辺の長さを出す
- 正方形である事を利用して、2辺の長さをイコールで結ぶ
- 座標を出す
たったこれだけです。
【超有料級】各学年の高校受験に向けた勉強方法にもまとめています!



一次関数の正方形を使った問題・解き方
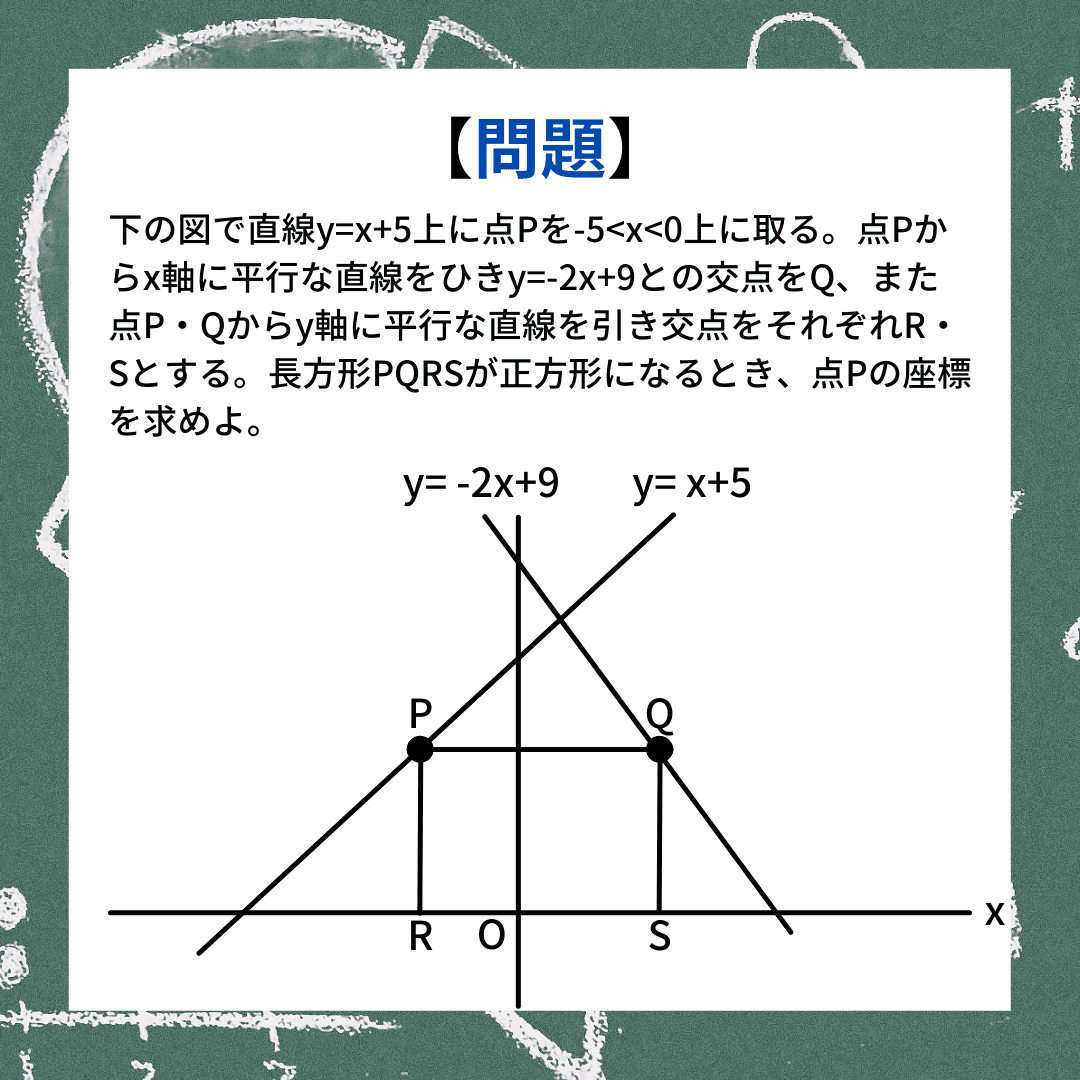
基本的な解き方の方針
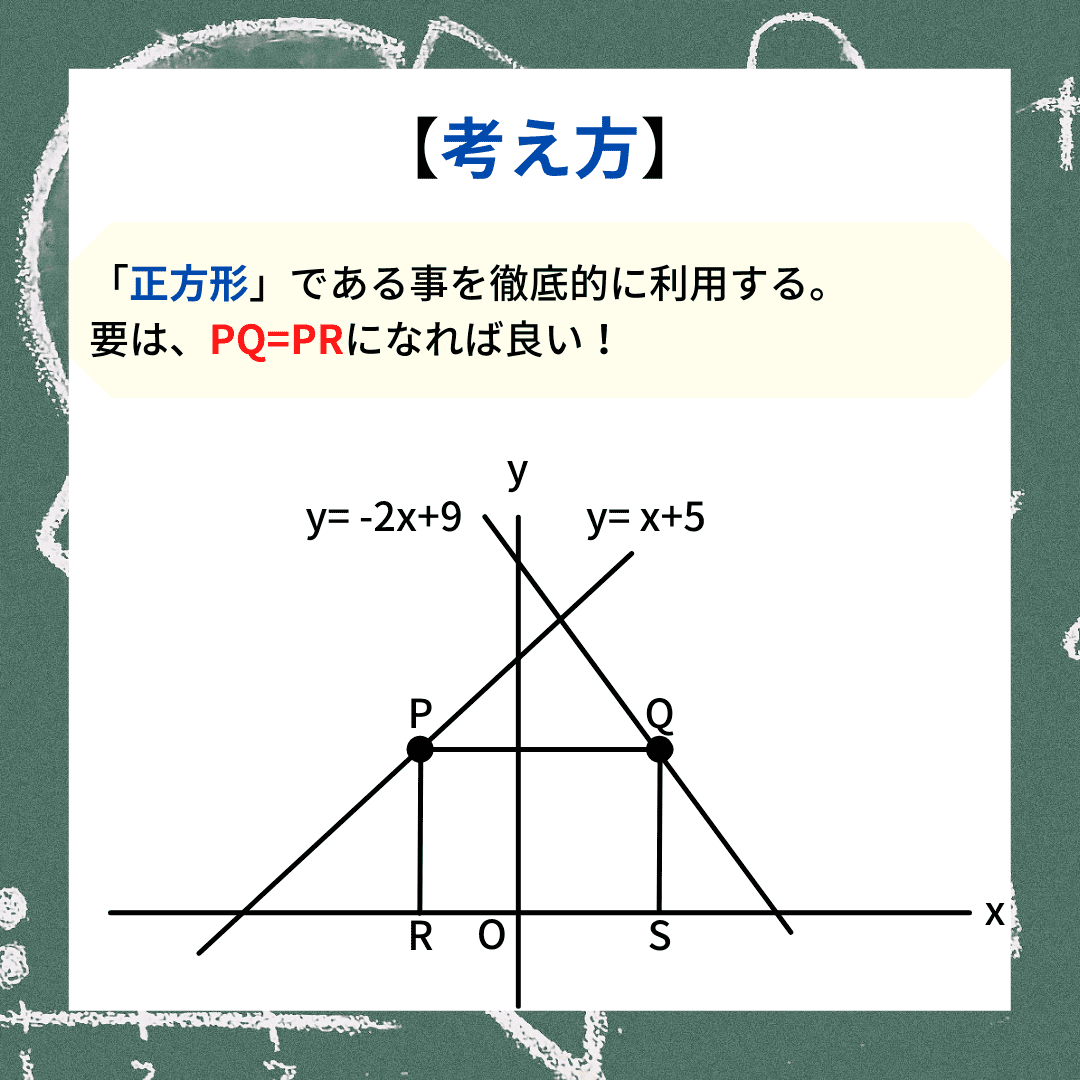 一次関数の正方形問題に対する考え方
一次関数の正方形問題に対する考え方長方形やひし形ではなく、あえて「正方形」を使っていることに注目しましょう。
正方形でなくてはいけない理由がそこにはあるわけです。
正方形は「全ての辺の長さが等しい」という最大の特徴を持っています。
この特徴を最大限に発揮していきます。
1.求めたい座標Pに文字を当てはめる
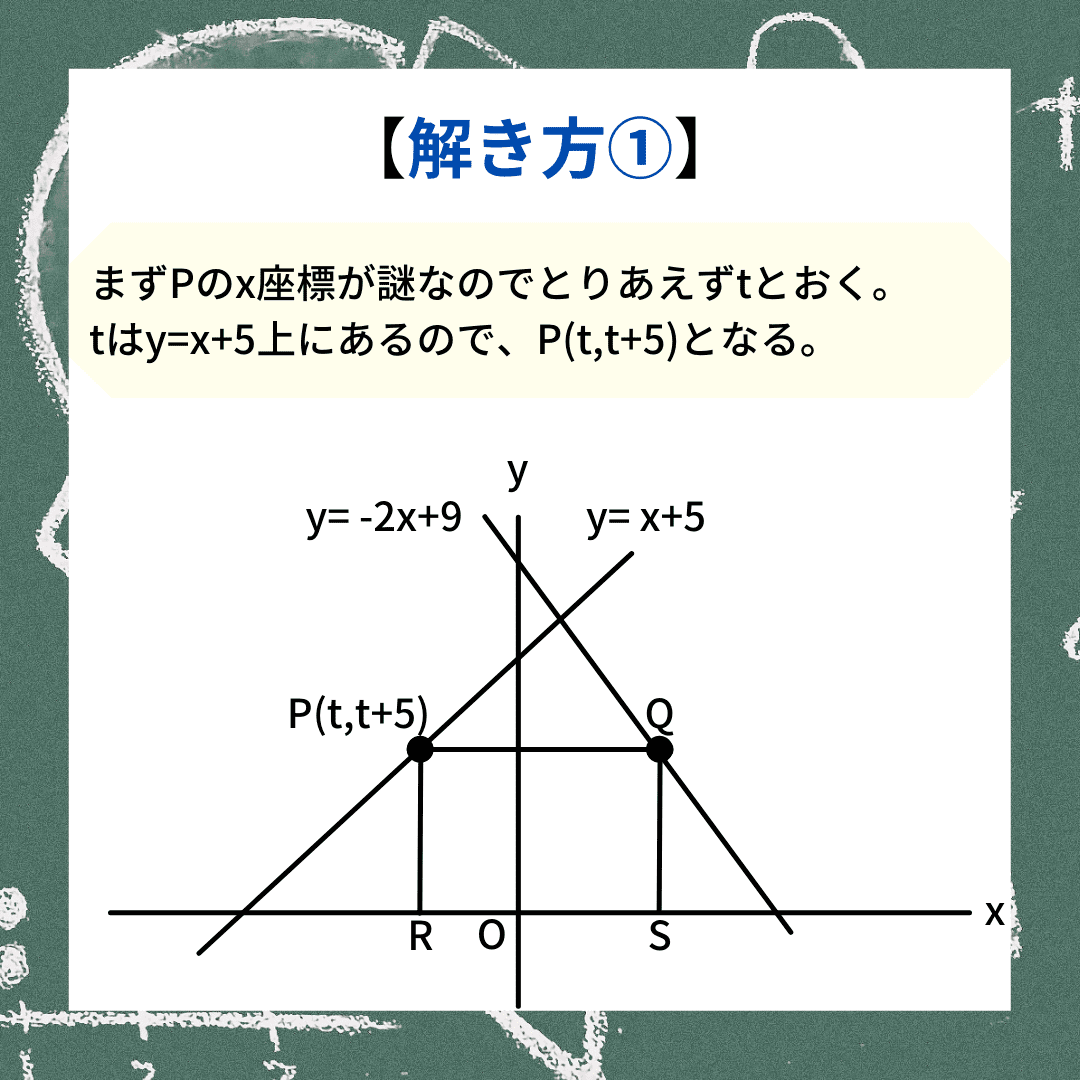 一次関数の正方形問題の説明①
一次関数の正方形問題の説明①最終的にPの座標を求めたいわけですから、まずはPのx座標を「t」とおきます。
Pはy=x+5上にあるので、y座標は「t+5」となります。
つまり、P(t,t+5)と置き換えることができます。
2.Qの座標を出す
 一次関数の正方形問題の説明②
一次関数の正方形問題の説明②次にQの座標を出していきます。
QはPと同じ高さにあるので、y座標「t+5」という事が分かります。
残るはx座標。Qはy=-2x+9上にあるのでyにt+5を代入して、t+5=-2x+9という式を作ります。ここから導き出されるxは「-1/2t+2」となります。
よって、Q(-1/2+2,t+5)となります。
3.PQの長さを出す
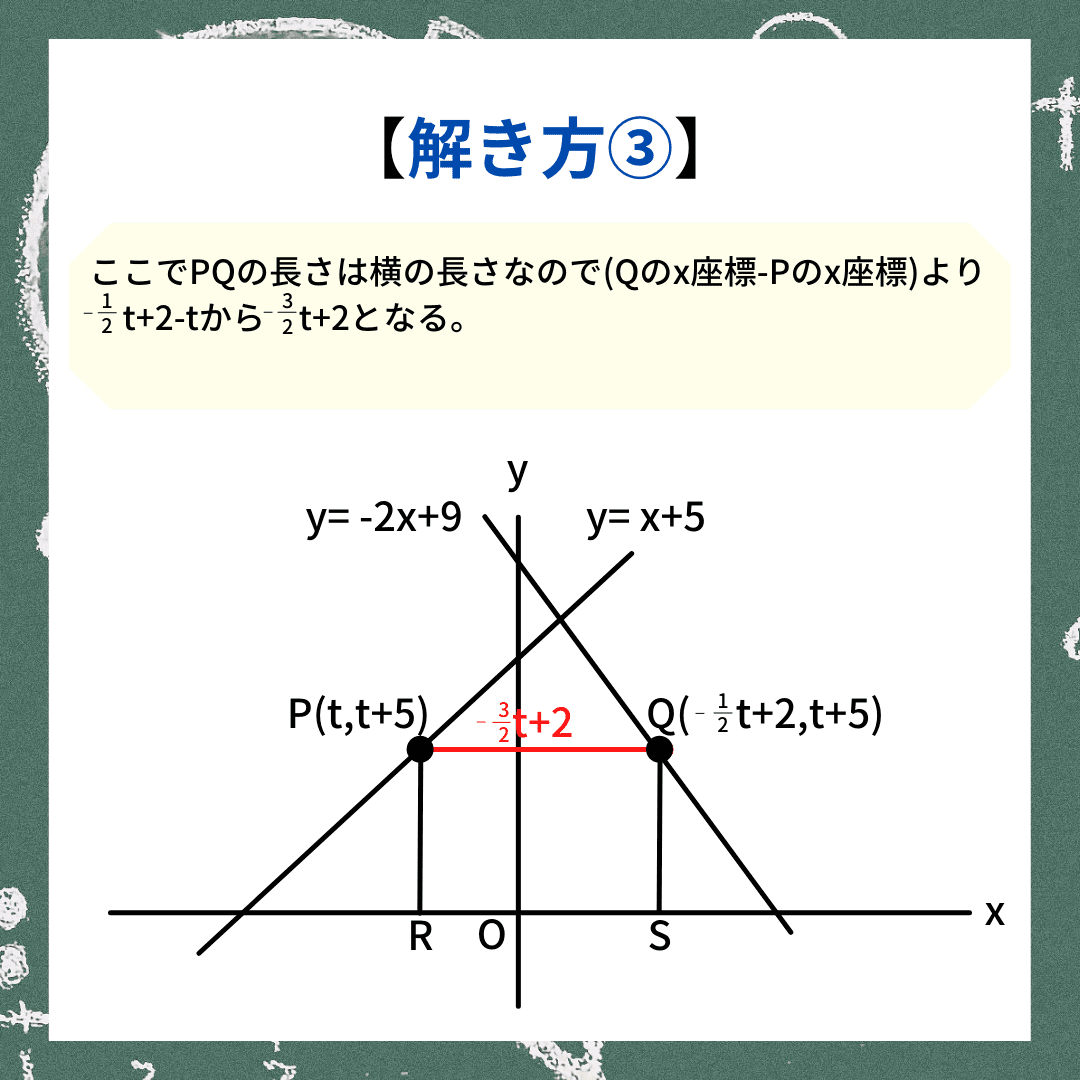 一次関数の正方形問題の説明③
一次関数の正方形問題の説明③では、PQの長さを出していきます。PQは横の長さなので、P・Qそれぞれのx座標に注目しましょう。
Pのx座標-Qのx座標より、PQ=-1/2t+2-tとなり、PQ=-3/2t+2
4.PRの長さを出す
 一次関数の正方形問題の説明④
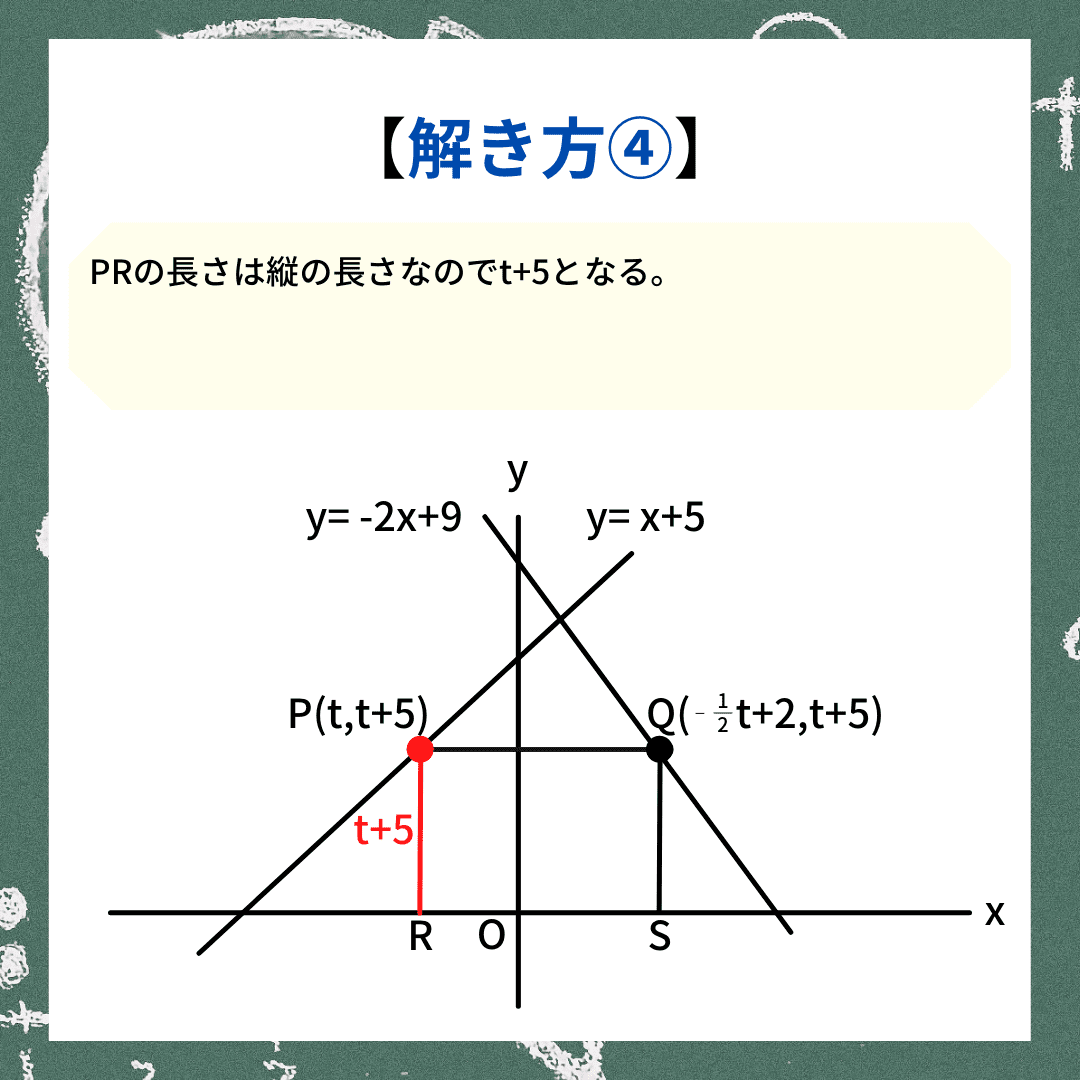
一次関数の正方形問題の説明④では、PRの長さを出していきます。PRは縦の長さなので、y座標に注目すれば良いですね。
Pのy座標は「t+5」なのでPR=t+5となります。
5.PQ=PRを解いてtの値を出す
 一次関数の正方形問題の説明⑤
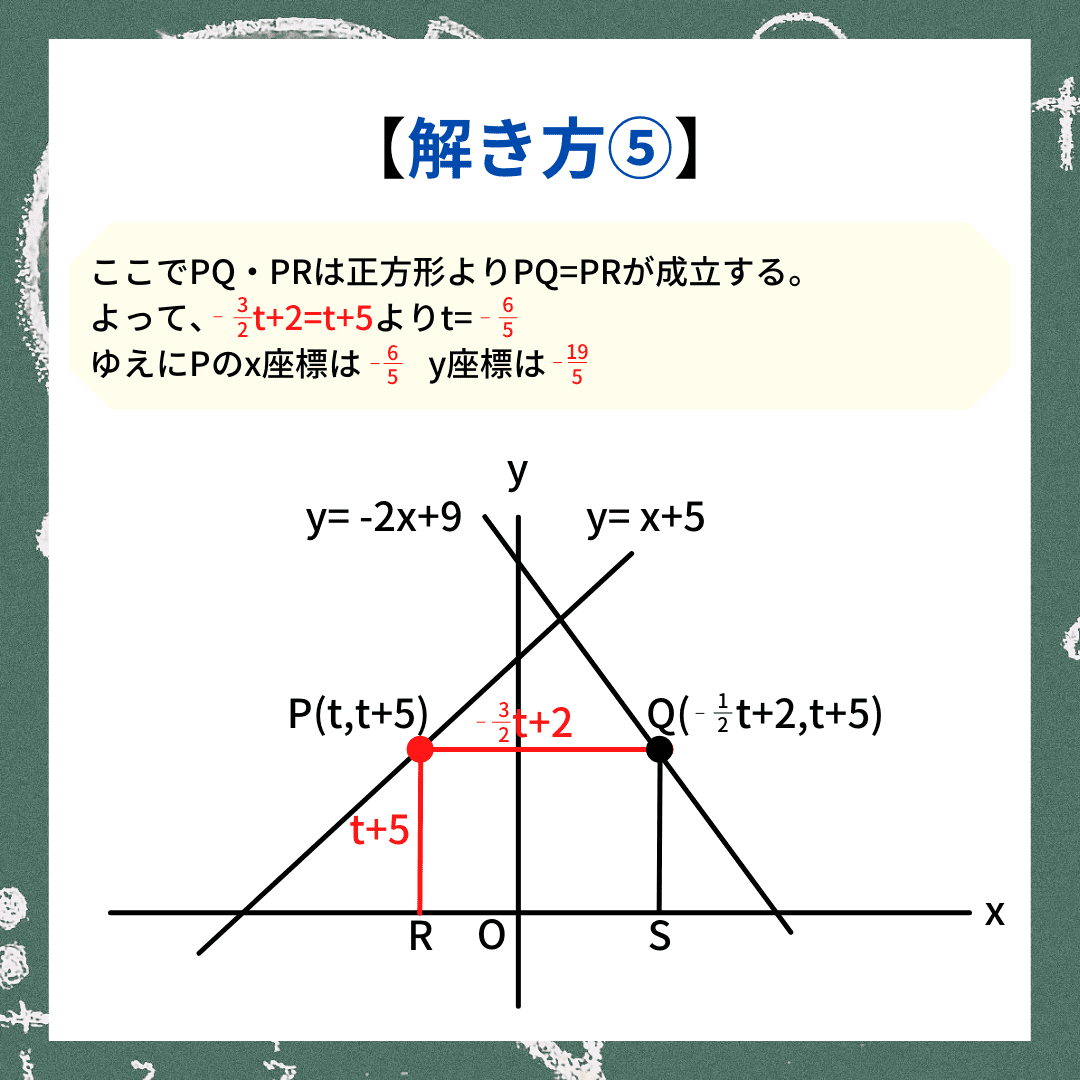
一次関数の正方形問題の説明⑤ここでPQRSは正方形より、PQ=PR。
よって、-3/2t+2=t+5が成立し、t=-6/5
6.答え
 一次関数の正方形問題の答え
一次関数の正方形問題の答えよって答えはP(-6/5,-19/5)となる。
一次関数の正方形問題の正答率
私が中学生向けの学習塾で教えている様子だと、中学2年生の初見正答率は3%ほどしかありません。
つまり、中学2年生にとっては問題として非常に難しい事が伺えます。
言い換えれば、問題に出て答えられるだけでも大きなアドバンテージになるということです。
公立高校入試における一次関数の正方形問題の傾向
公立高校入試において、一次関数の正方形問題の出題頻度は高くありません。
しかし、求めたい座標に文字(tなど)を当てはめて解法を導く手法は一次関数では一般的です。
出題頻度は高くありませんが、一次関数の正方形問題を解ければ粗方の対応は可能でしょう。
まとめ

以上が一次関数の正方形問題の解き方でした。
- 求めたい座標を文字で置き換える
- 方形を構成する各点の座標を求める
- 各辺の長さを出してイコールで結ぶ
- 文字の値を出す
一次関数の問題は難しいですが、問題はワンパターンで出る場合がほとんどです。
しっかり覚えた上で自信を持ってテストに挑めるようにしておきましょう。







.png)



